Transformada de Laplace

La transformada de Laplace es bastante usada en ingeniería y física. es un operador lineal que sirve para resolver ecuaciones diferenciales lineales. Mediante este método se puede convertir una ecuación diferencial lineal en una algebraica, que a su vez, permite el desarrollo del útil concepto de funciones de transferencia. 

La transformada de Laplace se define como:


La intregral esta definida entre:0≤t<∞. 

La letra s representa una variable positiva , en el proceso de integración se considera constante.

La transformada de Laplace convierte una función en terminos de t en una función en terminos de s.

Propiedades

Linealidad

Como la transformada de Laplace en una transformada integral, esta cumple con propiedades de linealidad.

Derivación

Primera derivada

Segunda derivada

Integración

Función de trasferencia

Donde R(s) es la entrada del sistema, C(s) la salida y G(s) es la función de trasferencia.

Funciones mas comunes

Función escalón unitario

Esta funcion es un cambio subito de magnitud unitaria en un tiempo igual a cero

Impulso unitario

En una función que representa un pulso ideal de amplitud infinita y duración cero, cuya área es la unidad

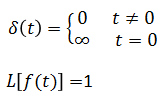
Página recomendada
Wolframalpha

Teoremas

Teorema de la traslación real

Es un teorema que trabaja con la traslación de una función en el eje del tiempo